Teorema de muestreo de Nyquist-Shannon
El teorema de muestreo de Nyquist-Shannon, también conocido como teorema de muestreo de Whittaker-Nyquist-Kotelnikov-Shannon, criterio de Nyquist o teorema de Nyquist , es un teorema fundamental de la teoría de la información, de especial interés en las telecomunicaciones.
Este teorema fue formulado en forma de conjetura por primera vez por Harry Nyquist en 1928 ("Certain topics in telegraph transmission theory"), y fue demostrado formalmente por Claude E. Shannon en 1949 ("Communication in the presence of noise").
El teorema trata con el muestreo, que no debe ser confundido o asociado con la cuantificación, proceso que sigue al de muestreo en la digitalización de una señal y que, al contrario del muestreo, no es reversible (se produce una pérdida de información en el proceso de cuantificación, incluso en el caso ideal teórico, que se traduce en una distorsión conocida como error o ruido de cuantificación y que establece un límite teórico superior a la relación señal-ruido). Dicho de otro modo, desde el punto de vista del teorema, las muestras discretas de una señal son valores exactos que aún no han sufrido redondeo o truncamiento alguno sobre una precisión determinada, esto es, aún no han sido cuantificadas.
El teorema demuestra que la reconstrucción exacta de una señal periódica continua en banda base a partir de sus muestras es matemáticamente posible si la señal está limitada en banda y la tasa de muestreo es superior al doble de su ancho de banda.
Dicho de otro modo, la información completa de la señal analógica original que cumple el criterio anterior está descrita por la serie total de muestras que resultaron del proceso de muestreo. No hay nada, por tanto, de la evolución de la señal entre muestras que no esté perfectamente definido por la serie total de muestras.
Si la frecuencia más alta contenida en una señal analógica  es
es  y la señal se muestrea a una tasa
y la señal se muestrea a una tasa 2F_{max} \equiv 2B \,\!" src="http://upload.wikimedia.org/math/5/0/1/501a05255370c3bf89259b7d66b614af.png" style="border-top-style: none; border-right-style: none; border-bottom-style: none; border-left-style: none; border-width: initial; border-color: initial; vertical-align: middle; margin-top: 0px; margin-right: 0px; margin-bottom: 0px; margin-left: 0px; ">, entonces
 se puede recuperar totalmente a partir de sus muestras mediante la siguiente función de interpolación:
se puede recuperar totalmente a partir de sus muestras mediante la siguiente función de interpolación:

Así,  se puede expresar como:
se puede expresar como:
 |
|---|
donde 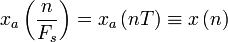 son las muestras de
son las muestras de  .
.
Hay que notar que el concepto de ancho de banda no necesariamente es sinónimo del valor de la frecuencia más alta en la señal de interés. A las señales para las cuales esto sí es cierto se les llama señales de banda base, y no todas las señales comparten tal característica (por ejemplo, las ondas de radio en frecuencia modulada).
Si el criterio no es satisfecho, existirán frecuencias cuyo muestreo coincide con otras (el llamado aliasing).

No hay comentarios:
Publicar un comentario